Cómo calcular la puntuación Z en Excel

En Excel, la puntuación z es una medida estadística que representa el número de desviaciones estándar que un punto de datos tiene de la media de un conjunto de datos. Para calcular el puntaje z en Excel, puede usar la función PRUEBA Z. Lo entendemos, es confuso, especialmente si no está familiarizado con las matemáticas, pero no se preocupe, profundizaremos en el cálculo de la puntuación z en Excel. Siga leyendo para descubrir cómo calcular el puntaje z en Excel y también para obtener información sobre el puntaje z inverso en Excel.

Cómo calcular la puntuación Z en Excel

Aquí, conocerá las formas de calcular la puntuación Z en Microsoft Excel.

¿Qué es la puntuación Z en Excel?

La puntuación z es una medida estadística que representa el número de desviaciones estándar. Se calcula restando la media del conjunto de datos del valor del punto de datos y luego dividiendo ese resultado por la desviación estándar del conjunto de datos. La puntuación z se puede utilizar para determinar si un valor es típico o inusual para el conjunto de datos. También se puede utilizar para comparar datos de diferentes conjuntos de datos mediante la estandarización de los datos.

Puede usar la función Z.TEST en Excel para calcular el puntaje z para un punto de datos específico, dado un rango de datos. Esto puede ser útil para identificar valores atípicos o inusuales en un conjunto de datos.

Se calcula mediante la siguiente fórmula:

puntuación z = (x – μ) / σ

dónde:

• x es el valor del punto de datos.
• μ es la media de los datos.
• σ es la desviación estándar de los datos.

Lea también:Cómo interpretar la puntuación Z

Cómo calcular la puntuación Z en Excel

Para calcular el puntaje z en Excel, puede usar el Estandarizado función. Veamos, con un ejemplo:

Suponga que estos son sus datos y desea encontrar la puntuación z.

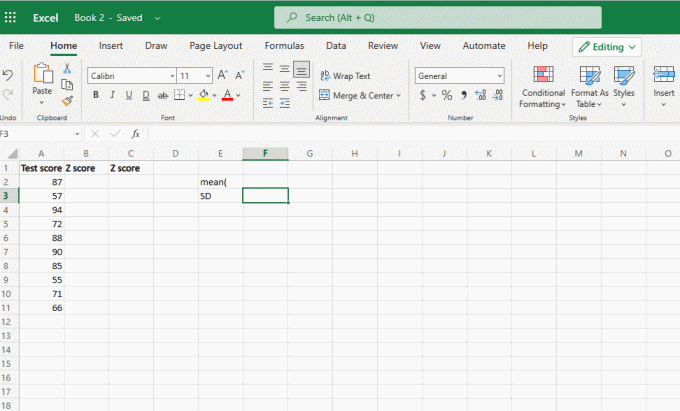
Ahora, siga los pasos para encontrar la puntuación z, pero primero debe encontrar la media y la desviación estándar.

Para calcular la media y la desviación estándar de sus datos. Siga los pasos que se mencionan a continuación.

1. Haga clic en la nueva celda y escriba promedio de igual.

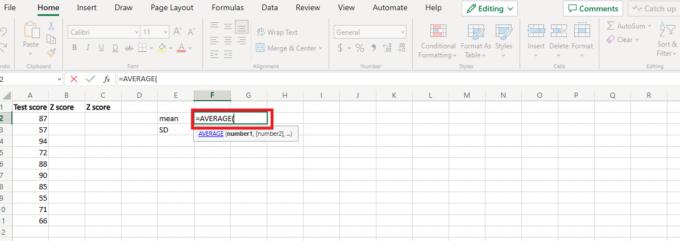
2. Haga clic y arrastre en todo el conjunto de datos y cierre el corchete.

3. presione el Introducir clave, y obtendrá su valor medio.

Ahora, para calcular la desviación estándar

1. Tipo es igual a DESVEST abra el corchete y seleccione nuevamente todos los datos.

2. Cierre el soporte y presione el Introducir clave.

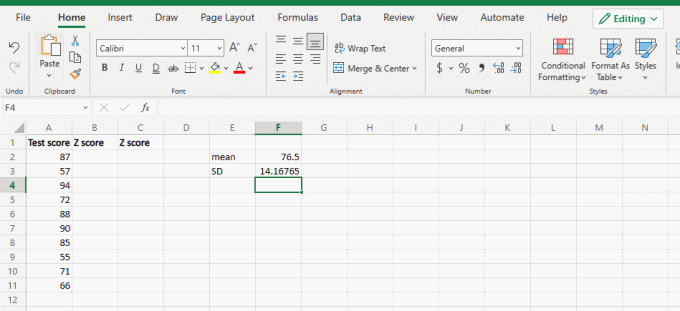
Entonces, aquí tienes tu desviación estándar

Ahora, calculemos el puntaje z para la primera celda

1. Haga clic en la nueva celda y escriba igual, el punto de datos, que es 87 en el ejemplo menos la media. Póngalos entre paréntesis, por lo que será (A2-F2) aquí dividido por la desviación estándar que es F3.

2. presione el Introducir clave, para obtener la puntuación z.

3. Ahora, para repetir lo mismo para todos los valores, agregue el signo $ en la fórmula (A2-$F$2)/$F$3 y luego simplemente arrastre hacia abajo y haga clic ctrl + D.

Nota: Agregar el prefijo de dólar ayuda a mantener estas dos celdas constantes al encontrar el valor de otras celdas.

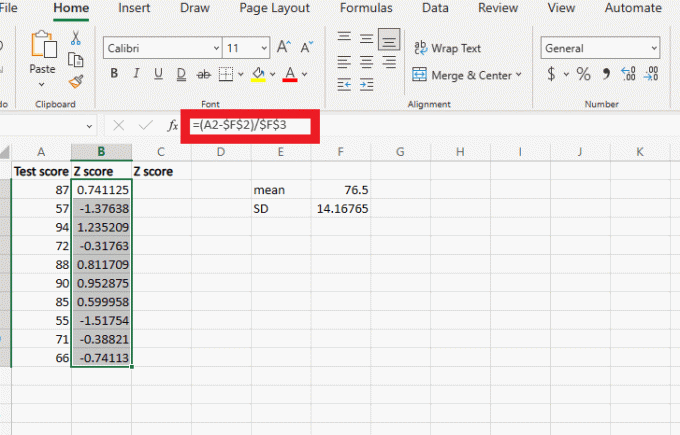
Ahora, tiene el valor de puntuación z para cada celda, espero que esto haya ayudado a aprender a calcular la puntuación z en Excel.

Lea también: Intercambiar columnas o filas en Excel

Cómo interpretar las puntuaciones Z en Excel

La desviación estándar de un valor de la media de un conjunto de datos se expresa como una puntuación z. La función Z.TEST en Excel se puede usar para determinar el puntaje z de un valor para un conjunto de datos dado.

Para interpretar el puntaje z, puede usar una tabla normal estándar (también conocida como tabla de puntaje z) para encontrar la probabilidad correspondiente. Por ejemplo, una puntuación z de 1,96 corresponde a una probabilidad de aproximadamente 0,975, lo que significa que el valor está dentro del 2,5 % superior de los datos. Por el contrario, una puntuación z de -1,96 corresponde a una probabilidad de aproximadamente 0,025, lo que significa que el valor se encuentra dentro del 2,5 % inferior de los datos.

También puede utilizar la tabla de puntuación z de Excel para determinar si un valor es un valor atípico en el conjunto de datos. Un valor con un puntaje z que es mucho más alto o más bajo que los otros valores en el conjunto de datos puede considerarse un valor atípico. Por ejemplo, puede considerar valores atípicos con puntuaciones z superiores a 3 o inferiores a -3. Es importante tener en cuenta que la interpretación de un puntaje z depende del contexto en el que se usa.

Lea también:Arreglar Excel lento para abrir en Windows 10

NORMA.S. Función INV en Excel

INV.NORM.S.ES una función de Microsoft Excel que devuelve el Excel de puntuación z inversa de la distribución acumulativa normal estándar. La distribución acumulativa normal estándar es una función que da la probabilidad de que una variable aleatoria, extraído de una distribución normal con media 0 y desviación estándar 1, es menor o igual que un valor.

Por ejemplo, si desea encontrar el valor que corresponde a una probabilidad de 0.9, usaría la siguiente fórmula:

=INV.NORM.S.(0.9)

La puntuación z inversa de Excel es útil para trabajar con la distribución normal estándar y la tabla Z. El puntaje Z inverso Excel le permite encontrar el valor que corresponde a una probabilidad dada, lo que puede ser útil para pruebas y procedimientos estadísticos que involucran la distribución normal estándar.

Preguntas frecuentes (FAQ)

Q1. ¿Qué te dice el puntaje z?

Respuesta Un puntaje z, también conocido como puntaje estándar, le indica cuántas desviaciones estándar se encuentra un valor de la media de un conjunto de datos. Una puntuación z puede ser positiva o negativa, dependiendo de si el valor está por encima o por debajo de la media.

Q2. ¿Por qué es tan importante el puntaje z?

Respuesta Los puntajes z son importantes porque le permiten comparar valores de diferentes conjuntos de datos estandarizándolos. Debido a que la puntuación z expresa el valor en términos de desviaciones estándar de la media, puede comparar valores que pueden tener diferentes unidades o escalas. Las puntuaciones z también son útiles para identificar valores atípicos en un conjunto de datos.

Q3. ¿Por qué se llama puntuación z?

Respuesta La puntuación z se llama puntuación z porque se basa en la distribución normal estándar, que es una distribución normal con una media de 0 y una desviación estándar de 1. La carta z se utiliza a menudo para denotar una variable aleatoria normal estándar.

Q4. ¿Qué es un buen valor de puntuación z?

Respuesta No tiene sentido hablar de un valor de puntuación z bueno o malo en general, porque la interpretación de una puntuación z depende del contexto en el que se utiliza.

P5. ¿Dónde se utilizan las puntuaciones z?

Respuesta Las puntuaciones z se utilizan en una amplia variedad de campos y aplicaciones. Los puntajes z a menudo se usan para evaluar el desempeño de los estudiantes en relación con sus compañeros. Por ejemplo, un maestro puede usar puntajes z para determinar qué estudiantes se están desempeñando por encima o por debajo del promedio para su nivel de grado.

P6. ¿Qué es la tabla z en Excel?

Respuesta La tabla de puntuación z de Excel, también conocida como tabla normal estándar, es una tabla de valores para la distribución normal estándar.

Recomendado:

• Reseñas de Jasper AI: detalles, precios y características
• Cómo establecer permisos de edición de hojas de cálculo de Google
• Cómo desbloquear las teclas de flecha en Excel
• Cómo desactivar el bloqueo de desplazamiento en Excel

Esperamos que este artículo haya sido útil para hacerle entender como calcular el puntaje z en excel. Lea el artículo y háganos saber si tiene alguna duda o consulta en la sección de comentarios a continuación.

Elon Decker

Elon es un escritor de tecnología en TechCult. Ha estado escribiendo guías prácticas durante aproximadamente 6 años y ha cubierto muchos temas. Le encanta cubrir temas relacionados con Windows, Android y los últimos trucos y consejos.