Hvordan tolke Z Score
Miscellanea / / April 05, 2023
En z-score er en numerisk måling som beskriver antall standardavvik for en bestemt verdi fra gjennomsnittet av et datasett. Den brukes til å bestemme hvor sjelden eller vanlig en bestemt verdi er i et datasett. Men hvordan finne z-score? Fortsett å lese artikkelen for å finne ut. En z-score kan være positiv eller negativ, der en positiv z-score indikerer at verdien er over gjennomsnittet og en negativ z-score indikerer at verdien er under gjennomsnittet. Vi vil diskutere hvordan du tolker z-score videre i artikkelen.

Innholdsfortegnelse
- Hvordan tolke Z Score
- Hva er Z Score?
- 1. Z-score er målt i standardavviksenheter
- 2. Z-score kan være positive eller negative
- 3. Z-score gjør det enkelt å sammenligne dataene dine med andre beregninger
- Hvordan finne Z Score
- Z-score vs standardavvik
- Hvordan tolke Z Score-tabell
- Hva betyr en negativ Z-score?
Hvordan tolke Z Score
I denne artikkelen vil du vite om trinnene for å tolke Z-score i detalj.
Hva er Z Score?
En z-score er en beregning som kvantifiserer hvor mange standardavvik en gitt verdi avviker fra datasettets gjennomsnitt. Den brukes til å fastslå sjeldenheten eller utbredelsen av en spesifikk verdi i et datasett. Fortsett å lese for å finne ut hvordan du tolker z-score
La oss se de mulige måtene å lære å tolke z-score på:
1. Z-score er målt i standardavviksenheter
Når du tolker en z-score, er det viktig å huske på at z-score måles i Standardavvik enheter. Dette betyr at verdien av z-score forteller deg hvor mange standardavvik en bestemt verdi er fra gjennomsnittet av datasettet.
Anta for eksempel at du har et datasett med et gjennomsnitt på 50 og et standardavvik på 10. Hvis du beregner z-skåren for en bestemt verdi, for eksempel 30, og finner at den er -2, kan du tolke dette som at verdien av 30 er to standardavvik under gjennomsnittet på 50.
Du kan også bruke en z-tabell for å bestemme prosentandelen av verdier i datasettet som er over eller under en bestemt z-score. Hvis du for eksempel har en z-score på 1,96, kan du slå opp denne verdien i en z-tabell for å finne at omtrent 97,5 % av verdiene i datasettet er under denne verdien.
2. Z-score kan være positive eller negative
Det faktum at z-score kan være positive eller negative er viktig når du tolker en z-score fordi det lar deg bestemme om en bestemt verdi er over eller under gjennomsnittet av datasettet og hvor sjelden eller vanlig denne verdien er i datasett. Videre i artikkelen vil du se hva en negativ z-score betyr
3. Z-score gjør det enkelt å sammenligne dataene dine med andre beregninger
z-score lar deg sammenligne dataene dine enkelt med andre beregninger som er viktig når du tolker en z-score fordi det lar deg sette dataene dine i kontekst og ta mer informerte beslutninger basert på dine analyse.
Les også: Fjern passord fra Excel-fil
Hvordan finne Z Score
For å finne z-skåren for en gitt verdi, må du vite gjennomsnittet og standardavviket til populasjonen eller utvalget som verdien kom fra. Z-score-beregningsformelen er som følger:
z = (x – gjennomsnitt) / standardavvik
Der x er verdien, er gjennomsnittet gjennomsnittet av populasjonen eller utvalget, og standardavviket er standardavviket til populasjonen eller utvalget.
La oss for eksempel si at du har et utvalg på 1000 personer, og du vil finne z-poengsummen for en person som er 6 fot høy. Gjennomsnittlig høyde på prøven er 5 fot, 10 tommer og standardavviket er 2 tommer. For å beregne z-poengsummen for en person som er 6 fot høy, bruker du følgende formel:
z = (72 – 70) / 2 = 1
Dette vil bety at personen som er 6 fot høy er ett standardavvik over gjennomsnittet.
Hvis du vil finne z-skåren for en verdi som er under gjennomsnittet, vil z-skåren være negativ. For eksempel, hvis verdien er 5 fot, 8 tommer, vil z-poengsummen være:
z = (68 – 70) / 2 = -1
Dette vil bety at personen som er 5 fot, 8 tommer er ett standardavvik under gjennomsnittet.
Z-score vs standardavvik
Nedenfor er noen av forskjellene mellom z-score vs standardavvik.
| Z-score | Standardavvik |
| Antall standardavvik et datapunkt er fra gjennomsnittet | Et mål på spredningen eller spredningen av et sett med datapunkter rundt gjennomsnittet |
| Formelen for z-poengsum er. (x – gjennomsnitt) / standardavvik |
Formelen for standardavvik er. √((Σ(x – gjennomsnitt)^2) / n) |
| Forteller deg hvor mange standardavvik et datapunkt er fra gjennomsnittet | Forteller deg hvor spredt dataene er fra gjennomsnittet |
| En z-score på 1,5 betyr at datapunktet er 1,5 standardavvik over gjennomsnittet | Et standardavvik på 10 betyr at datapunktene vanligvis er 10 enheter unna gjennomsnittet |
Så, hovedforskjellen mellom z-score vs standardavvik er at en z-score er et spesifikt mål på hvordan mange standardavvik er en verdi fra gjennomsnittet, mens dataspredningen er kvantifisert ved standardavvik.
Les også: Bytt raskt mellom regneark
Hvordan tolke Z Score-tabell
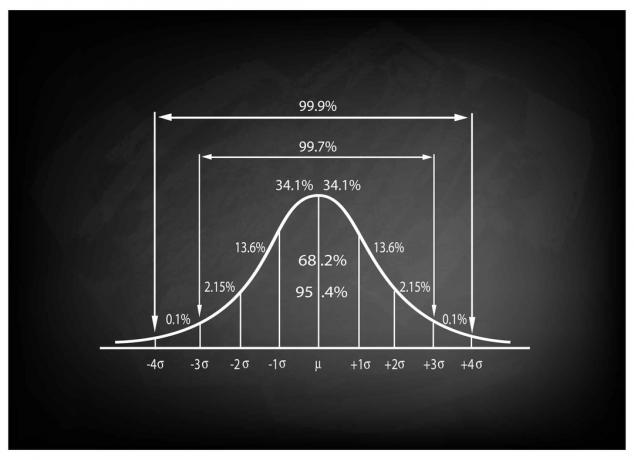
For å lære å tolke z-score-tabellen, må du først vite z-score-verdien for verdien du vil slå opp. Z-score-tabellen vil vanligvis vise deg området under standard normalkurven for et gitt område av z-score.
La oss for eksempel si at du vil finne området under kurven for en z-score på 1,5. Du ville se i z-score tabell for raden som tilsvarer z-skåren på 1,5, og finn deretter kolonnen som tilsvarer arealet under kurve. Verdien i den cellen er arealet under kurven for en z-score på 1,5.
Arealet under kurven er sannsynligheten for at en gitt verdi inntreffer. For eksempel, hvis arealet under kurven for en z-score på 1,5 er 0,9332, så er det 93,32 % sannsynlighet for at en verdi med en z-score på 1,5 vil oppstå.
Det er viktig å merke seg at z-score-tabeller vanligvis er basert på standard normalkurven, som er en normalfordeling med et gjennomsnitt på 0 og et standardavvik på 1. Hvis z-score er basert på et annet gjennomsnitt og standardavvik, må du bruke en z-score konverteringsformel for å konvertere den til standard normalfordeling før du slår den opp i bord.
Les også: Hvordan endre brukernavn og navn på Clubhouse Android
Hva betyr en negativ Z-score?
En negativ z-score betyr at verdien er mindre enn gjennomsnittet. Det er med andre ord under gjennomsnittet.
For bedre forståelse, la oss ta det forrige eksemplet og si at du har et utvalg på 1000 personer, og du vil finne z-score for en person som er 5 fot, 8 tommer høy. Gjennomsnittlig høyde på prøven er 5 fot, 10 tommer, og standardavviket er 2 tommer. For å beregne z-poengsummen for en person som er 5 fot, 8 tommer høy, bruker du følgende formel:
z = (68 – 70) / 2 = -1
Dette vil bety at personen som er 5 fot, 8 tommer høy er ett standardavvik under gjennomsnittet.
Generelt betyr en z-score på 0 at en verdi er nøyaktig på gjennomsnittet, en z-score på 1 betyr at en verdi er én standardavvik over gjennomsnittet, og en z-score på -1 betyr at en verdi er ett standardavvik under mener.
Ofte stilte spørsmål (FAQs)
Q1. Hvordan brukes Z-Score i det virkelige liv?
Ans. Z-skåren, også referert til som standardskåren, er en beregning for å bestemme hvor mange standardavvik et tall er fra datasettets gjennomsnitt. Å finne uteliggere, anomalier og merkelige mønstre i data er en typisk oppgave innen statistikk, dataanalyse og maskinlæring.
Q2. Hva ville gi en negativ z-score?
Ans. En negativ Z-score indikerer at en verdi er under gjennomsnittet av datasettet. Generelt vil enhver verdi som er mindre enn gjennomsnittet av datasettet gi en negativ Z-score.
Q3. Hva forteller Z-tabellen deg?
Ans. Z-tabellen, også kjent som standard normaltabell, er en statistisk tabell som viser sannsynligheten for at en gitt verdi forekommer innenfor en standard normalfordeling.
Anbefalt:
- Slik ser du slettede YouTube-videoer
- En komplett guide til Modbus-slaveprinsippet
- Hvordan INDEKSERE MATCH flere kriterier i Google Sheets
- Hvordan fungerer GNSS?
For å tolke en Z-score er det viktig å vurdere gjennomsnittet og standardavviket til datasettet, samt konteksten Z-skåren brukes i. Vi håper inderlig at vi kan gi litt informasjon om hvordan tolke z-score. Gi oss beskjed om dine spørsmål og forslag i kommentarfeltet nedenfor.

Elon Decker
Elon er en teknisk skribent ved TechCult. Han har skrevet veiledninger i ca. 6 år nå og har dekket mange emner. Han elsker å dekke emner relatert til Windows, Android og de nyeste triksene og tipsene.



