Hur man tolkar Z Score
Miscellanea / / April 05, 2023
En z-poäng är ett numeriskt mått som beskriver antalet standardavvikelser för ett visst värde från medelvärdet av en datauppsättning. Det används för att bestämma hur sällsynt eller vanligt ett visst värde är i en datauppsättning. Men hur hittar man z-poäng? Fortsätt läsa artikeln för att ta reda på det. En z-poäng kan vara positiv eller negativ, där en positiv z-poäng indikerar att värdet ligger över medelvärdet och ett negativt z-värde indikerar att värdet ligger under medelvärdet. Vi kommer att diskutera hur man tolkar z-poäng vidare i artikeln.

Innehållsförteckning
- Hur man tolkar Z Score
- Vad är Z Score?
- 1. Z-poäng mäts i standardavvikelseenheter
- 2. Z-poäng kan vara positiva eller negativa
- 3. Z-scores gör det enkelt att jämföra dina data med andra mätvärden
- Hur man hittar Z Score
- Z-poäng vs standardavvikelse
- Hur man tolkar Z-poängtabellen
- Vad betyder ett negativt Z-resultat?
Hur man tolkar Z Score
I den här artikeln kommer du att veta om stegen för att tolka Z-poäng i detalj.
Vad är Z Score?
Ett z-poäng är ett mått som kvantifierar hur många standardavvikelser ett givet värde avviker från datasetets medelvärde. Den används för att fastställa sällsyntheten eller förekomsten av ett specifikt värde inom en datauppsättning. Fortsätt läsa för att ta reda på hur du tolkar z-poäng
Låt oss se de möjliga sätten att lära sig att tolka z-poäng:
1. Z-poäng mäts i standardavvikelseenheter
När man tolkar en z-poäng är det viktigt att tänka på att z-poäng mäts in Standardavvikelse enheter. Detta betyder att värdet på z-poängen talar om hur många standardavvikelser ett visst värde är från medelvärdet av datamängden.
Anta till exempel att du har en datauppsättning med ett medelvärde på 50 och en standardavvikelse på 10. Om du beräknar z-poängen för ett visst värde, säg 30, och finner att det är -2, kan du tolka detta som att värdet på 30 är två standardavvikelser under medelvärdet av 50.
Du kan också använda en z-tabell för att bestämma procentandelen av värden i datamängden som är över eller under en viss z-poäng. Om du till exempel har ett z-poäng på 1,96 kan du slå upp det här värdet i en z-tabell för att se att cirka 97,5 % av värdena i datamängden ligger under detta värde.
2. Z-poäng kan vara positiva eller negativa
Det faktum att z-poäng kan vara positiva eller negativa är viktigt när man tolkar ett z-poäng eftersom det låter dig avgöra om ett visst värde ligger över eller under medelvärdet för datasetet och hur sällsynt eller vanligt det värdet är i dataset. Längre fram i artikeln kommer att se vad en negativ z-poäng betyder
3. Z-scores gör det enkelt att jämföra dina data med andra mätvärden
z-poäng gör att du enkelt kan jämföra dina data med andra mätvärden, vilket är viktigt när du tolkar en z-score eftersom det låter dig sätta din data i ett sammanhang och fatta mer välgrundade beslut baserat på dina analys.
Läs också: Ta bort lösenord från Excel-fil
Hur man hittar Z Score
För att hitta z-poängen för ett givet värde måste du känna till medelvärdet och standardavvikelsen för populationen eller urvalet som värdet kom från. Formeln för z-poängberäkning är följande:
z = (x – medelvärde) / standardavvikelse
Där x är värdet, är medelvärdet medelvärdet av populationen eller urvalet, och standardavvikelsen är standardavvikelsen för populationen eller urvalet.
Låt oss till exempel säga att du har ett urval på 1000 personer och du vill hitta z-poängen för en person som är 6 fot lång. Medelhöjden för provet är 5 fot, 10 tum och standardavvikelsen är 2 tum. För att beräkna z-poängen för en person som är 6 fot lång, skulle du använda följande formel:
z = (72 – 70) / 2 = 1
Detta skulle innebära att personen som är 6 fot lång är en standardavvikelse över medelvärdet.
Om du vill hitta z-poängen för ett värde som ligger under medelvärdet blir z-poängen negativ. Till exempel, om värdet är 5 fot, 8 tum, skulle z-poängen vara:
z = (68 – 70) / 2 = -1
Detta skulle innebära att personen som är 5 fot, 8 tum är en standardavvikelse under medelvärdet.
Z-poäng vs standardavvikelse
Nedan listas några av skillnaderna mellan z-poäng vs standardavvikelse.
| Z poäng | Standardavvikelse |
| Antalet standardavvikelser en datapunkt är från medelvärdet | Ett mått på spridningen eller spridningen av en uppsättning datapunkter runt medelvärdet |
| Formeln för z-poäng är. (x – medelvärde) / standardavvikelse |
Formeln för standardavvikelse är. √((Σ(x – medel)^2) / n) |
| Talar om hur många standardavvikelser en datapunkt är från medelvärdet | Berättar hur spridda uppgifterna är från medelvärdet |
| Ett z-värde på 1,5 betyder att datapunkten är 1,5 standardavvikelser över medelvärdet | En standardavvikelse på 10 betyder att datapunkterna vanligtvis ligger 10 enheter från medelvärdet |
Så den största skillnaden mellan z-poäng vs standardavvikelse är att en z-poäng är ett specifikt mått på hur många standardavvikelser är ett värde från medelvärdet, medan dataspridningen kvantifieras genom standardavvikelse.
Läs också: Växla snabbt mellan arbetsblad
Hur man tolkar Z-poängtabellen
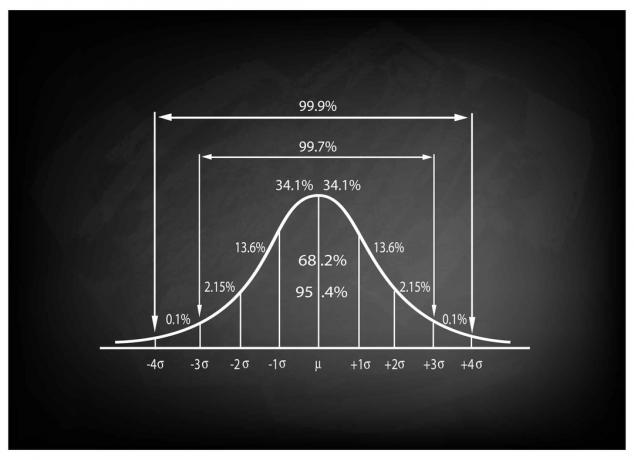
För att lära dig hur du tolkar z-poängtabellen måste du först veta z-poängen för det värde du vill slå upp. Z-poängtabellen kommer vanligtvis att visa dig arean under standardnormalkurvan för ett givet intervall av z-poäng.
Låt oss till exempel säga att du vill hitta arean under kurvan för en z-poäng på 1,5. Du skulle titta i z-poängen tabell för raden som motsvarar z-poängen 1,5, och hitta sedan kolumnen som motsvarar arean under kurva. Värdet i den cellen är arean under kurvan för en z-poäng på 1,5.
Arean under kurvan är sannolikheten för att ett givet värde inträffar. Till exempel, om arean under kurvan för en z-poäng på 1,5 är 0,9332, så finns det en 93,32 % sannolikhet att ett värde med en z-poäng på 1,5 kommer att inträffa.
Det är viktigt att notera att z-poängtabeller vanligtvis är baserade på standardnormalkurvan, som är en normalfördelning med ett medelvärde på 0 och en standardavvikelse på 1. Om ditt z-poäng är baserat på ett annat medelvärde och standardavvikelse måste du använda ett z-poäng omvandlingsformel för att konvertera den till standardnormalfördelningen innan du slår upp den i tabell.
Läs också: Hur man ändrar användarnamn och namn på Clubhouse Android
Vad betyder ett negativt Z-resultat?
En negativ z-poäng betyder att värdet är mindre än medelvärdet. Det är med andra ord under medelvärdet.
För bättre förståelse, låt oss ta det föregående exemplet och säga att du har ett urval på 1000 personer och att du vill hitta z-poängen för en person som är 5 fot, 8 tum lång. Medelhöjden för provet är 5 fot, 10 tum och standardavvikelsen är 2 tum. För att beräkna z-poängen för en person som är 5 fot, 8 tum lång, skulle du använda följande formel:
z = (68 – 70) / 2 = -1
Detta skulle innebära att personen som är 5 fot, 8 tum lång är en standardavvikelse under medelvärdet.
I allmänhet betyder en z-poäng på 0 att ett värde är exakt vid medelvärdet, en z-poäng på 1 betyder att ett värde är ett standardavvikelse över medelvärdet, och en z-poäng på -1 betyder att ett värde är en standardavvikelse under betyda.
Vanliga frågor (FAQs)
Q1. Hur används Z-Score i verkliga livet?
Ans. Z-poängen, även kallad standardpoängen, är ett mått för att bestämma hur många standardavvikelser ett tal är från datasetets medelvärde. Att hitta extremvärden, anomalier och konstiga mönster i data är en typisk uppgift inom statistik, dataanalys och maskininlärning.
Q2. Vad skulle ge en negativ z-poäng?
Ans. Ett negativt Z-värde indikerar att ett värde ligger under medelvärdet av datamängden. I allmänhet kommer alla värden som är mindre än medelvärdet av datamängden att ge ett negativt Z-poäng.
Q3. Vad säger Z-tabellen dig?
Ans. Z-tabellen, även känd som standardnormaltabellen, är en statistisk tabell som visar sannolikheten för att ett givet värde inträffar inom en standardnormalfördelning.
Rekommenderad:
- Hur man tittar på raderade YouTube-videor
- En komplett guide till Modbus-slavprincipen
- Hur man INDEXERA MATCHAR flera kriterier i Google Sheets
- Hur fungerar GNSS?
För att tolka en Z-poäng är det viktigt att överväga medelvärdet och standardavvikelsen för datamängden, såväl som det sammanhang där Z-poängen används. Vi hoppas verkligen att vi kan ge lite information om hur man tolkar z-poäng. Låt oss veta dina frågor och förslag i kommentarsfältet nedan.

Elon Decker
Elon är en teknisk skribent på TechCult. Han har skrivit instruktionsguider i cirka 6 år nu och har täckt många ämnen. Han älskar att ta upp ämnen relaterade till Windows, Android och de senaste tricken och tipsen.



